| SISTEMA DIÉDRICO: INTERSECCIONES | |||||
INTERSECCIÓN ENTRE PLANOS CUYAS TRAZAS NO SE CORTAN DENTRO DE LOS LÍMITES DEL PAPEL |
|||||
| Ni las trazas verticales ni las horizontales se cortan dentro de los límites del papel | |||||
En este caso empleamos dos planos auxiliares uno de ello será paralelo al horizontal y el otro paralelo a uno de los planos (podemos utilizar dos planos horizontales, dos planos frontales o uno horizontal y otro frontal) |
|||||
1º Dibujamos el plano paralelo al horizontal y hallamos su intersección con los dos planos obteniendo el punto A (a'-a) 2º Trazamos un plano paralelo al plano P, hallando su intersección con el plano Q. Esta intersección será paralela a la intersección entre los planos dados 3º Solo queda dibujar las paralelas a la recta auxiliar hallada en el paso anterior en el punto A |
|||||
En el caso de que las trazas verticales u horizontales sean paralelas En este caso la intersección será paralela a ellas, dando como resultado una horizontal o frontal del plano. |
|||||
|
|||||
| INTERSECCIÓN ENTRE RECTA Y PLANO | |||||
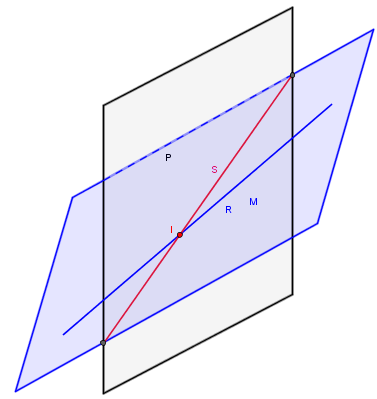
| Aspectos generales De la intersección entre una recta y un plano obtenemos como resultado un punto, que pertenece a ambos elementos, para hallarlo se procede de la siguiente manera: 1º Contenemos la recta dada (R)
en un plano auxiliar (M); los planos más utilizados en estos casos son los
proyectantes. 2º Se halla la intersección del plano auxiliar con el principal, dando como resultado una recta (S). 3º La intersección entre la recta dada (R) y la hallada (S) da como resultado el punto (I) de intersección. |
 |
||||
| Como contener las diferentes rectas en planos | |||||
Esta operación es muy sencilla y conviene saber en cuantos planos se puede contener una misma recta, ya que a veces por la posición de la recta dentro del formato, solo podremos utilizar uno concreto. |
|||||
|
|||||