Pág. 1

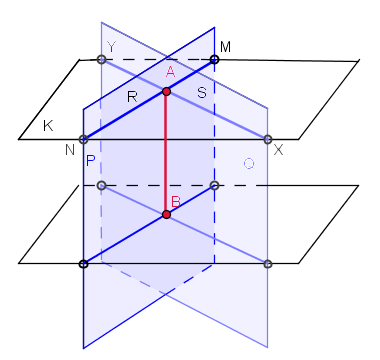
La intersección entre dos planos será una recta que pertenece a ambos planos y queda definida cuando se unen dos de sus puntos. Para hallar los puntos que nos definen la recta intersección en el espacio, nos ayudamos de dos planos auxiliares, que cortan a los planos anteriores para definiendo la recta intersección.
Si observamos la figura, el plano auxiliar K corta al plano P en los puntos N y M, que unidos nos definen la recta R; del mismo modo, corta al plano Q en los puntos X e Y, cuya unión es la recta S. El corte de las rectas R y S será uno de los puntos que necesitamos para determinar la recta intersección de los dos planos principales, el punto A.

La operación se repite con otro plano auxiliar para hallar el segundo punto. Teniendo en cuenta que en el sistema diédrico los planos auxiliares son el vertical y el horizontal de proyección, el ejercicio se reduce a hallar la intersección de las trazas homónimas de los planos, ya que las trazas de la recta se encuentran en las intersecciones de las trazas de dichos planos.

Intersección entre planos oblicuos

Como explicamos en el apartado anterior hallamos la intersección de las trazas homónimas de los planos, es decir:

1º Donde P'y Q' se corten se encuentra la traza vertical de la recta (v')

2º La traza horizontal (h) es la intersección de las trazas horizontales de los planos  P y Q

3º Se proyectan sobre la línea de tierra v y h'. Para determinar la recta basta unir las trazas homónimas

si mueves los puntos azules podrás variar la posición del plano

Se aplica el mismo método expuesto anteriormente, pero para localizar la intersección de las trazas deberemos prolongarlas hasta que se corten.

La recta intersección de un plano oblicuo cualquiera y de un plano horizontal ha de ser horizontal ya que por pertenecer al plano horizontal tiene que ser paralela y  a su vez horizontal del plano por pertenecer al plano oblicuo.

Pág. 1