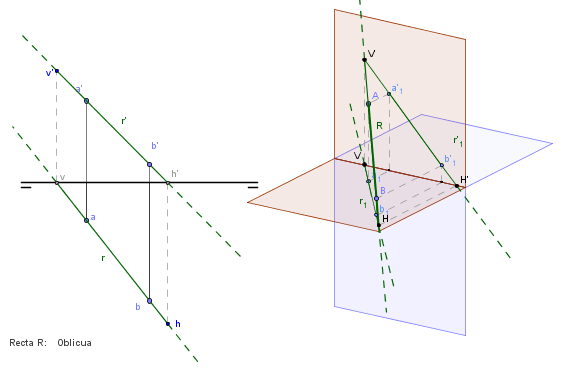
Una recta situada en el espacio queda definida sobre un plano por todas las proyecciones de los puntos que la componen. En el sistema diédrico nos basta con dos de sus proyecciones para poder definirla. Como el sistema diédrico está formado por dos planos de proyección esos dos puntos tendrán cuatro proyecciones (las verticales y las horizontales), uniendo las del mismo signo, es decir, las homónimos conseguiremos repersentar la recta en este sistema.

Imagina que la recta R está representada por los puntos A y B.  Estos puntos se transforman en el sistema diédrico en las siguientes proyecciones: a´,a, b´,b. Para poder dibujarla uniremos (a´) con (b´) dando como resultado de esta unión, la proyección vertical de la recta (r´); y (b) con (a) trazando de esta manera la proyección horizontal de la recta (r).

Trazas o puntos notables de una recta

Pues bien, como la recta se puede representar por dos de sus infinitos puntos; está podrá ser definida por las trazas.
Se llaman trazas de una recta a  los puntos resultantes de la intersección de la recta con los planos de proyección. Esta intersección  da como resultado dos trazas:

• Traza horizontal (H). Es el punto de la recta que corta al plano horizontal de proyección, al estar contenido en el palno horizontal su proyección horizontal será h confundida con el mismo punto, es decir contenida en ese mismo plano, por lo tanto, su proyección vertical será h´,   contenida en la línea de tierra.

• Traza vertical (V). Es el punto de intersección de la recta con el plano vertical de proyección. Su proyección vertical v´, estará contenido en ese mismo plano, y su proyección horizontal  sobre la línea de tierra v.
  

Como digimos en un principio los planos bisectores dividen los cuadrantes en dos partes iguales, por lo que estos serán atravesados por las rectas. En su intersección obtendremos otros puntos considerados a su vez como puntos notables o trazas.

Cuando la recta corta al primer bisector, obtendremos un punto que estará contenido en él, cuya cota y alejamiento tienen la misma distancia y se sitúan uno a cada lado de la línea de tierra.

Cuando la recta corta al segundo bisector, obtendremos un punto  contenido en él, cuya cota y alejamiento tienen la misma distancia y sus proyecciones se encuentran coincidentes por encima de lla línea de tierra o por de bajo de la misma.

Como consecuencia de la situación del espectador (1º Cuadrante), la parte de la recta que se halle en dicho cuadrante será vista, es decir sólo la porción de la recta limitada por sus trazas. Una vez que la recta atraviese los planos de proyección y pase a otros cuadrantes ésta se considerará oculta.

La parte vista de la recta se representa con trazo grueso continuo y la parte oculta con trazo grueso discontinuo.

Alfabeto de la recta

Aunque son infinitas las posiciones  en el espacio, solo tres serán las que pueden adoptar respecto los elementos del sistema, es decir los planos y la línea de tierra  (oblicua, paralela y perpendicular). Con lo que el alfabeto de la recta se compone de 53 posiciones.

• Recta oblicua. En el sistema diédrico se estudian cuatro casos generales de rectas que atraviesan tres cuadrantes y dos que cortan a la LT.